Le charme des équations

"On ne peut échapper au sentiment que ces formules mathématiques possèdent une existence indépendante et une intelligence qui leur est propre, qu’elles sont plus sages que nous, plus sages même que leurs découvreurs, que nous en tirons davantage que ce qu’on y a mis à l’origine", Henrich R. Hertz (1857-1894).

On le sait, ceux qu’on appelle les mathophobes frémissent à la seule vue d’une formule mathématique; aussi l’idée que les équations puissent avoir une vie propre suffit à leur donner des convulsions. Pourtant, c’est un fait : non seulement ces formules ont-elles une histoire fascinante, mais elles ouvrent en outre une voie royale en histoire des sciences, entre autres en physique. C’est, en tout cas, la thèse défendue par Robert P. Crease dans son ouvrage, The Great Equations¹.Il n’est pas le premier à proposer une telle approche. Dans The Emperor’s New Mind (Oxford Univ. Press, 1989), le mathématicien britannique Roger Penrose avait identifié sept grandes théories axiomatisées dans l’histoire de la physique mathématique, lesquelles constituaient, selon lui, de rares moments de grâce. Les Éléments d’Euclide ayant évidemment servi de modèle, il en dressait la liste suivante :

• la statique d’Archimède;
• la dynamique newtonienne;
• la théorie électromagnétique de Maxwell;
• les deux moutures successives de la théorie de la relativité, restreinte et générale;
• la première élaboration de la mécanique quantique;
• la QED, l’électrodynamique quantique.

Pour sa part, Crease retient aussi les équations des étapes 3, 4 et 5, mais il y ajoute le théorème de Pythagore, la deuxième Loi de la thermodynamique, ainsi que l’équation d’Euler souvent considérée comme la plus élégante de l’histoire :

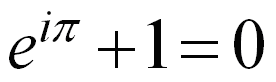
Enfin, il identifie deux équations centrales dans la Dynamique newtonienne, la deuxième Loi du mouvement (F = ma) et la Loi de la gravitation universelle, de même que dans la Mécanique quantique, soit l’équation de Schrödinger décrivant l’évolution d’un système quantique et les célèbres relations d’incertitude d’Heisenberg. Dans cet ouvrage assez original, chacune hérite d’un chapitre développé, expliquant à la fois son origine, sa signification et sa portée.

Souffrez-vous d’anosognosie?

Pourquoi aborder l’histoire des sciences à partir des équations? C’est que Crease épouse l’optique du physicien allemand Hertz (1857-1894) : « On ne peut échapper au sentiment que ces formules mathématiques possèdent une existence indépendante et une intelligence qui leur est propre, qu’elles sont plus sages que nous, plus sages même que leurs découvreurs, que nous en tirons davantage que ce qu’on y a mis à l’origine » (cité p.147)².

Bien qu’assez originale, cette approche ne prétend pas renouveler le genre, non plus d’ailleurs que défendre une thèse inédite en épistémologie ou en histoire des sciences . Non, Crease vise autre chose. Écoutons-le citer par exemple le célèbre passage de l’ouvrage de C. P. Snow, The Two Cultures (1959) : « Souvent, j’ai assisté à des rencontres de gens qui, d’après les standards de la culture traditionnelle [la culture humaniste], étaient considérés comme très éduqués, et qui exprimaient vivement leur incrédulité devant l’absence de culture des scientifiques. Une fois ou deux, on m’a provoqué et j’ai alors demandé aux personnes présentes combien d’entre elles pouvaient décrire la deuxième Loi de la thermodynamique. La réponse fut aussi froide que négative. Pourtant, je demandais quelque chose qui est à peu près l’équivalent scientifique de la question : "Avez-vous déjà lu une pièce de Shakespeare?"» (p. 111).

Tout comme Snow, Crease veut bâtir un pont entre les deux cultures. Il s’étonne par exemple que l’on puisse, comme Howard Zinn, dont A People’s History of the United States fait autorité, écrire l’histoire d’un pays sans dire un mot des découvertes scientifiques qui l’ont marqué ou même de certaines innovations techniques qui ont changé la vie des gens (pp. 152-155). Il déplore la même chose chez certains romanciers dont les personnages, dit-il, semblent tout ignorer du monde technologique ambiant. Tous ces gens souffrent, à son avis, d’anosognosie, c’est-à-dire d’un syndrome (du grec nosos) qui les rend aussi ignorants (agnosie) qu’inconscients de leur état (anosos). Crease aimerait faire de son ouvrage un remède apte à soigner ce syndrome au nom volontairement provocateur. Il croit en effet que, loin d’affaiblir les humanités, une guérison de leurs symptômes les plus criants ne pourrait que leur être bénéfique. Au vu de l’intérêt de son effort, il est difficile d’être en désaccord.

Élégance de style pour équations

On s’en doute, un tel essai, farci par la force des choses de formules mathématiques, aurait pu s’avérer aussi aride que rebutant. Pourtant, le tout se lit au contraire avec grand plaisir. C’est que le style de Crease est aussi élégant que ses explications sont éclairantes. Illustrons le tout par un exemple, le chapitre 6 consacré aux travaux de Maxwell.

Le style de Crease est aussi élégant que ses explications sont éclairantes.

Ce scientifique écossais a, on s’en souvient, unifié en un domaine cohérent les phénomènes optiques, électriques et magnétiques, auparavant autonomes. Il a exposé l’ensemble de ses résultats dans son indigeste Treatise on Electricity and Magnetism, publié en deux forts volumes (1873). Aussi, de la vingtaine d’équations majeures que comporte ce traité déterminant, a-t-on tiré quatre formules qui constituent encore la base de l’enseignement de l’électromagnétisme dans les manuels contemporains de physique collégiale³. 

Crease parvient à rendre ses travaux accessibles, d’abord en situant Maxwell dans son contexte, puis en exposant l’état dispersé des connaissances de l’époque avant son intervention décisive. Il explique ensuite de quelle façon Maxwell en est peu à peu venu à entrevoir sa grande synthèse. C’est l’occasion de rappeler qu’en créant les concepts décisifs de champ et d’onde électromagnétiques, il a ouvert la voie à Einstein. En effet, on lui doit l’hypothèse dont partira ce dernier, à savoir que la lumière, ce phénomène en apparence si mystérieux, est simplement, au fond, une onde électromagnétique. Or, c’est en éliminant l’éther et en faisant de la vitesse de la lumière un invariant qu’Einstein bouleversera de fond en comble les équations de la Dynamique classique, créant ainsi la théorie de la Relativité restreinte. Notons au passage que l’une des autres activités scientifiques de Maxwell fut la fondation du célèbre Laboratoire Cavendish (1874), dont il fut le premier « Cavendish Professor of Experimental Physics ». Or, on connait le rôle éminent joué par ce laboratoire dans l’histoire ultérieure des sciences⁴.

J’ai donné l’exemple de Maxwell, mais Crease procède de manière analogue pour l’ensemble des équations retenues. Dans certains cas, dont celui de la thermodynamique, le récit devient particulièrement dramatique. En effet, sans doute est-ce le domaine scientifique dont le développement exigea le plus lourd tribut. Ainsi, l’ingénieur français Sadi Carnot (1796-1832), le premier à expliquer les principes déterminant le fonctionnement d’une machine à vapeur et à ouvrir en conséquence la voie à ce nouveau champ d’investigation , mourut à 36 ans, dans un asile. Il était atteint du choléra. Le médecin et physicien allemand Robert Mayer (1814-1878) y finit, lui aussi, ses jours, la camisole de force et l’internement l’attendant après qu’il se soit défenestré. Depuis des années, il essayait, sans succès, de faire reconnaître sa paternité dans la découverte de la deuxième Loi de la thermodynamique, liée aux variations de l’entropie. Quant à l’Autrichien Ludwig Boltzmann (1844-1906), enfin, il fut totalement incompris à son époque et finit par se suicider de désespoir. Considéré comme l’un des fondateurs de la Mécanique statistique, ses travaux font pourtant aujourd’hui autorité. En son honneur, on a d’ailleurs donné son nom à une importante constante physique.

Cette façon de démystifier les mathématiques est-elle bienvenue? Oui, à cause de leur rôle exceptionnel dans le monde actuel.

On peut soigner la mathophobie

Cette façon de démystifier les mathématiques est-elle bienvenue? Oui, à cause de leur rôle exceptionnel dans le monde actuel. En effet, la maîtrise de nombre d’enjeux cruciaux suppose une familiarité minimale avec les chiffres, qu’on examine les données sur les changements climatiques, les développements de l’informatique ou encore les nanotechnologies. Évidemment, il n’est pas nécessaire que tout un chacun devienne un crack en la matière. Après tout, pour des gens profondément allergiques, ne pas être un analphabète numérique relève déjà de l’exploit. Mais pour bienvenue qu’elle soit, cette démystification des mathématiques est-elle efficace? Selon moi, tout à fait. Car les formules s’enchaînent tout naturellement et les notions plus difficiles sont expliquées de manière graduelle. Ainsi, en prenant le lecteur par la main et en le guidant pas à pas, si je puis dire, l’auteur arrive à rendre compréhensibles ces équations célèbres et à lui en faire goûter tout le sel. Ce faisant, il réussit son pari : montrer que l’allergie au formalisme n’est nullement incurable. Enfin, ajoutons qu’en faisant de l’histoire des sciences une excitante aventure intellectuelle, il insuffle la vie aux équations et rend plus humaines les mathématiques elles-mêmes.

Mathématiques et citoyenneté

À propos, ai-je dit que Crease lui-même n’est nullement mathématicien? En fait, il dirige le département de philosophie de l’Université Stony Brook, à New York. Aussi son ouvrage est-il une illustration vivante du principe qui guide, depuis le début, cette chronique de culture scientifique. En effet, selon moi, les connaissances humaines ne prennent tout leur sens que dans le contexte culturel qui leur a donné naissance et les maintient vivantes. En contrepartie, on ne saurait, dans le monde actuel, envisager la culture en écartant les sciences ou leur ancrage le plus ferme, les mathématiques. Mieux même, on ne saurait comprendre les forces à l’œuvre dans la société et, partant, y participer efficacement, sans la maîtrise de quelques concepts de base. Autrement dit, aujourd’hui plus que jamais, les sciences, et particulièrement les mathématiques, constituent l’adjuvant le plus solide d’une citoyenneté pleine et entière. Aussi, plus que bienvenus, des outils comme celui de Crease sont-ils indispensables.

À propos, ai-je dit que Crease lui-même n’est nullement mathématicien? En fait, il dirige le département de philosophie de l’Université Stony Brook, à New York.

Notes et références :

• 1. The Great Equations. Breakthroughs in Science from Pythagoras to Heisenberg, New York, W. W. Norton & Cy, 2008.
• 2. Toutes les traductions de l’ouvrage reproduites dans ce bref texte sont celles de l'auteur.
• 3. Ce travail de synthèse et d’épuration a été réalisé par l’ingénieur, mathématicien et physicien britannique Oliver Heaviside (1850-1925). Mais, comme le signale Crease (p. 142, n. 10), Maxwell avait lui-même indiqué la voie permettant de condenser ses équations dans un article de 1868, qui présentait ce qu’il appelait les quatre théorèmes fondamentaux du nouveau champ scientifique.  
• 4. À ce propos, voir notre chronique de février 2012, Un laboratoire pas comme les autres.